Assembly
language programming develops a very basic and low level understanding of the
computer. In higher level languages there is a distance between the computer
and the programmer. This is because higher level languages are designed to be
closer and friendlier to the programmer, thereby creating distance with the
machine. This distance is covered by translators called compilers and
interpreters. The aim of programming in assembly language is to bypass these
intermediates and talk directly with the computer.
There is a general impression that
assembly language programming is a difficult chore and not everyone is capable
enough to understand it. The reality is in contrast, as assembly language is a
very simple subject. The wrong impression is created because it is very
difficult to realize that the real computer can be so simple. Assembly language
programming gives a freehand exposure to the computer and lets the programmer
talk with it in its language. The only translator that remains between the
programmer and the computer is there to symbolize the computer’s numeric world
for the ease of remembering.
To cover
the practical aspects of assembly language programming, IBM PC based on Intel
architecture will be used as an example. However this course will not be tied
to a particular architecture as it is often done. In our view such an approach
does not create versatile assembly language programmers. The concepts of
assembly language that are common across all platforms will be developed in
such a manner as to emphasize the basic low level understanding of the computer
instead of the peculiarities of one particular architecture. Emphasis will be
more on assembly language and less on the IBM PC.
Before attempting this course you
should know basic digital logic operations of AND, OR, NOT etc. You should know
binary numbers and their arithmetic. Apart from these basic concepts there is
nothing much you need to know before this course. In fact if you are not an
expert, you will learn assembly language quickly, as non-experts see things
with simplicity and the basic beauty of assembly language is that it is
exceptionally simple. Do not ever try to find a complication, as one will not
be there. In assembly language what is written in the program is all that is
there, no less and no more.
After
successful completion of this course, you will be able to explain all the basic
operations of the computer and in essence understand the psychology of the
computer. Having seen the computer from so close, you will understand its
limitations and its capabilities. Your logic will become fine grained and this
is one of the basic objectives of teaching assembly language programming.
Then
there is the question that why should we learn assembly language when there are
higher level languages one better than the other; C, C++, Java, to name just a
few, with a neat programming environment and a simple way to write programs.
Then why do we need such a freehand with the computer that may be dangerous at
times? The answer to this lies in a very simple example. Consider a translator
translating from English to Japanese. The problem faced by the translator is
that every language has its own vocabulary and grammar. He may need to
translate a word into a sentence and destroy the beauty of the topic. And given
that we do not know
Japanese, so we cannot verify that
our intent was correctly conveyed or not. Compiler is such a translator, just a
lot dumber, and having a scarce number of words in its target language, it is
bound to produce a lot of garbage and unnecessary stuff as a result of its
ignorance of our program logic. In normal programs such garbage is acceptable
and the ease of programming overrides the loss in efficiency but there are a
few situations where this loss is unbearable.
Think about a four color picture
scanned at 300 dots per inch making 90000 pixels per square inch. Now a
processing on this picture requires 360000 operations per square inch, one
operation for each color of each pixel. A few extra instructions placed by the
translator can cost hours of extra time. The only way to optimize this is to do
it directly in assembly language. But this doesn’t mean that the whole
application has to be written in assembly language, which is almost never the
case. It’s only the performance critical part that is coded in assembly
language to gain the few extra cycles that matter at that point.
Consider an arch just like the ones
in mosques. It cannot be made of big stones alone as that would make the arch
wildly jagged, not like the fine arch we are used to see. The fine grains of
cement are used to smooth it to the desired level of perfection. This operation
of smoothing is optimization. The core structure is built in a higher level
language with the big blocks it provides and the corners that need optimization
are smoothed with the fine grain of assembly language which allows extreme
control.
Another
use of assembly language is in a class of time critical systems called real
time systems. Real time systems have time bound responses, with an upper limit
of time on certain operations. For such precise timing requirement, we must
keep the instructions in our total control. In higher level languages we cannot
even tell how many computer instructions were actually used, but in assembly
language we can have precise control over them. Any reasonable sized
application or a serious development effort has nooks and corners where
assembly language is needed. And at these corners if there is no assembly
language, there can be no optimization and when there is no optimization, there
is no beauty. Sometimes a useful application becomes useless just because of
the carelessness of not working on these jagged corners.
The third major reason for learning
assembly language and a major objective for teaching it is to produce fine
grained logic in programmers. Just like big blocks cannot produce an arch, the
big thick grained logic learnt in a higher level language cannot produce the
beauty and fineness assembly language can deliver. Each and every grain of
assembly language has a meaning; nothing is presumed (e.g. div and mul for
input and out put of decimal number). You have to put together these grains,
the minimum number of them to produce the desired outcome. Just like a “for”
loop in a higher level language is a block construct and has a hundred things
hidden in it, but using the grains of assembly language we do a similar
operation with a number of grains but in the process understand the minute
logic hidden beside that simple “for” construct.
Assembly
language cannot be learnt by reading a book or by attending a course. It is a
language that must be tasted and enjoyed. There is no other way to learn it.
You will need to try every example, observe and verify the things you are told
about it, and experiment a lot with the computer. Only then you will know and
become able to appreciate how powerful, versatile, and simple this language is;
the three properties that are hardly ever present together.
Whether
you program in C/C++ or Java, or in any programming paradigm be it object
oriented or declarative, everything has to boil down to the bits and bytes of
assembly language before the computer can even understand it.
1.1. BASIC COMPUTER
ARCHITECTURE
Address, Data, and
Control Buses
A
computer system comprises of a processor, memory, and I/O devices. I/O is used
for interfacing with the external world, while memory is the processor’s
internal world. Processor is the core in this picture and is responsible for
performing operations. The operation of a computer can be fairly described with
processor and memory only. I/O will be discussed in a later part of the course.
Now the whole working of the computer is performing an operation by the
processor on data, which resides in memory.
The scenario
that the processor executes operations and the memory contains data elements
requires a mechanism for the processor to read that data from the memory. “That
data” in the previous sentence much be rigorously explained to the memory which
is a dumb device. Just like a postman, who must be told the precise address on
the letter, to inform him where the destination is located. Another significant
point is that if we only want to read the data and not write it, then there
must be a mechanism to inform the memory that we are interested in reading data
and not writing it. Key points in the above discussion are:
•
There
must be a mechanism to inform memory that we want to do the read operation
•
There
must be a mechanism to inform memory that we want to read precisely which
element
•
There
must be a mechanism to transfer that data element from memory to processor
The
group of bits that the processor uses to inform the memory about which element
to read or write is collectively known as the address bus. Another
important bus called the data bus is used to move the data from the
memory to the processor in a read operation and from the processor to the
memory in a write operation. The third group consists of miscellaneous
independent lines used for control purposes. For example, one line of the bus
is used to inform the memory about whether to do the read operation or the
write operation. These lines are collectively known as the control bus.
These
three buses are the eyes, nose, and ears of the processor. It uses them in a
synchronized manner to perform a meaningful operation. Although the programmer
specifies the meaningful operation, but to fulfill it the processor needs the
collaboration of other units and peripherals. And that collaboration is made available
using the three buses. This is the very basic description of a computer and it
can be extended on the same lines to I/O but we are leaving it out just for
simplicity for the moment.
The
address bus is unidirectional and address always travels from processor to
memory. This is because memory is a dumb device and cannot predict which
element the processor at a particular instant of time needs. Data moves from
both, processor to memory and memory to processor, so the data bus is
bidirectional. Control bus is special and relatively complex, because different
lines comprising it behave differently. Some take
information
from the processor to a peripheral and some take information from the
peripheral to the processor. There can be certain events outside the processor
that are of its interest. To bring information about these events the data bus
cannot be used as it is owned by the processor and will only be used when the
processor grants permission to use it. Therefore certain processors provide
control lines to bring such information to processor’s notice in the control
bus. Knowing these signals in detail is unnecessary but the general idea of the
control bus must be conceived in full.
We
take an example to explain the collaboration of the processor and memory using
the address, control, and data buses. Consider that you want your uneducated
servant to bring a book from the shelf. You order him to bring the fifth book
from top of the shelf. All the data movement operations are hidden in this one
sentence. Such a simple everyday phenomenon seen from this perspective explains
the seemingly complex working of the three buses. We told the servant to “bring
a book” and the one which is “fifth from top,” precise location even for the
servant who is much more intelligent then our dumb memory. The dumb servant
follows the steps one by one and the book is in your hand as a result. If
however you just asked him for a book or you named the book, your uneducated
servant will stand there gazing at you and the book will never come in your
hand.
Even
in this simplest of all examples, mathematics is there, “fifth from top.”
Without a number the servant would not be able to locate the book. He is unable
to understand your will. Then you tell him to put it with the seventh book on
the right shelf. Precision is involved and only numbers are precise in this
world. One will always be one and two will always be two. So we tell in the
form of a number on the address bus which cell is needed out of say the 2000
cells in the whole memory.
A binary number is generated on the address bus, fifth,
seventh, eighth, tenth; the cell which is needed. So the cell number is placed
on the address bus. A memory cell is an n- bit location to store data, normally
8-bit also called a byte. The number of bits in a cell is called the cell
width. The two dimensions, cell width and number of cells, define the
memory completely just like the width and depth of a well defines it completely.
200 feet deep by 15 feet wide and the well is completely described. Similarly
for memory we define two dimensions. The first dimension defines how many
parallel bits are there in a single memory cell. The memory is called 8-bit or
16-bit for this reason and this is also the word size of the memory. This need
not match the size of a processor word which has other parameters to define it.
In general the memory cell cannot be wider than the width of the data bus. Best
and simplest operation requires the same size of data bus and memory cell
width.
As we previously discussed that the control bus carries
the intent of the processor that it wants to read or to write. Memory changes
its behavior in response to this signal from the processor. It defines the
direction of data flow. If processor wants to read but memory wants to write,
there will be no communication or useful flow of information. Both must be
synchronized, like a speaker speaks and the listener listens. If both speak
simultaneously or both listen there will be no communication. This precise
synchronization between the processor and the memory is the responsibility of
the control bus.
Control
bus is only the mechanism. The responsibility of sending the appropriate
signals on the control bus to the memory is of the processor. Since the memory
never wants to listen or to speak of itself. Then why is the control bus
bidirectional. Again we take the same example of the servant and the book
further to elaborate this situation. Consider that the servant went to fetch
the book just to find that the drawing room door is locked. Now the servant can
wait there indefinitely keeping us in surprise or come back and inform us about
the situation so that we can act accordingly. The servant even though he was
obedient was unable to fulfill our orders so in all his obedience, he came back
to inform us about the problem. Synchronization is still important, as a result
of our orders either we got the desired cell or we came to know that the memory
is locked for the moment. Such information cannot be transferred via the
address or the data bus. For such situations when peripherals want to talk to
the processor when the processor wasn’t expecting them to speak, special lines
in the control bus are used. The information in such signals is usually to
indicate the incapability of the peripheral to do something for the moment. For
these reasons the control bus is a bidirectional bus and can carry information
from processor to memory as well as from memory to processor.
1.2. REGISTERS
The
basic purpose of a computer is to perform operations, and operations need
operands. Operands are the data on which we want to perform a certain
operation. Consider the addition operation; it involves adding two numbers to
get their sum. We can have precisely one address on the address bus and
consequently precisely one element on the data bus. At the very same instant
the second operand cannot be brought inside the processor. As soon as the
second is selected, the first operand is no longer there. For this reason there
are temporary storage places inside the processor called registers. Now
one operand can be read in a register and added into the other which is read
directly from the memory. Both are made accessible at one instance of time, one
from inside the processor and one from outside on the data bus. The result can
be written to at a distinct location as the operation has completed and we can
access a different memory cell. Sometimes we hold both operands in registers
for the sake of efficiency as what we can do inside the processor is
undoubtedly faster than if we have to go outside and bring the second operand.
Registers
are like a scratch pad ram inside the processor and their operation is very
much like normal memory cells. They have precise locations and remember what is
placed inside them. They are used when we need more than one data element
inside the processor at one time. The concept of registers will be further
elaborated as we progress into writing our first program.
Memory is a limited resource but the number of memory
cells is large. Registers are relatively very small in number, and are
therefore a very scarce and precious resource. Registers are more than one in
number, so we have to precisely identify or name them. Some manufacturers
number their registers like r0, r1, r2, others name them like A, B, C, D etc.
Naming is useful since the registers are few in number. This is called the
nomenclature of the
particular
architecture. Still other manufacturers name their registers according to their
function like X stands for an index register. This also informs us that there
are special functions of registers as well, some of which are closely
associated to the particular architecture. For example index registers do not
hold data instead they are used to hold the address of data. There are other
functions as well and the whole spectrum of register functionalities is quite
large. However most of the details will become clear as the registers of the
Intel architecture are discussed in detail.
Accumulator
There is a central register in every processor called the
accumulator. Traditionally all mathematical and logical operations are
performed on the accumulator. The word size of a processor is defined by the
width of its accumulator. A 32bit processor has an accumulator of 32 bits.
Pointer, Index, or Base Register
The
name varies from manufacturer to manufacturer, but the basic distinguishing
property is that it does not hold data but holds the address of data. The
rationale can be understood by examining a “for” loop in a higher level
language, zeroing elements in an array of ten elements located in consecutive
memory cells. The location to be zeroed changes every iteration. That is the
address where the operation is performed is changing. Index register is used in
such a situation to hold the address of the current array location. Now the
value in the index register cannot be treated as data, but it is the address of
data. In general whenever we need access to a memory location whose address is
not known until runtime we need an index register. Without this register we
would have needed to explicitly code each iteration separately.
In newer architectures the distinction between accumulator
and index registers has become vague. They have general registers which are
more versatile and can do both functions. They do have some specialized
behaviors but basic operations can be done on all general registers.
Flags Register or Program Status Word
This is a special register in every architecture called
the flags register or the program status word. Like the accumulator it is an 8,
16, or 32 bits register but unlike the accumulator it is meaningless as a unit,
rather the individual bits carry different meanings. The bits of the
accumulator work in parallel as a unit and each bit mean the same thing. The
bits of the flags register work independently and individually, and combined
its value is meaningless.
An example of a bit commonly present in the flags register
is the carry flag. The carry can be contained in a single bit as in binary
arithmetic the carry can only be zero or one. If a 16bit number is added to a
16bit accumulator, and the result is of 17 bits the 17th bit is placed in the
carry bit of the flags register. Without this 17th bit the answer is incorrect.
More examples of flags will be discussed when dealing with the Intel specific
register set.
Program Counter or Instruction Pointer
Everything must translate into a binary number for our
dumb processor to understand it, be it an operand or an operation itself.
Therefore the instructions themselves must be translated into numbers. For
example to add numbers we understand the word “add.” We translate this word
into a number to make the processor understand it. This number is the actual
instruction for the computer. All the objects, inheritance and encapsulation
constructs in higher level languages translate down to just a number in
assembly language in the end. Addition, multiplication, shifting; all big
programs
are made using these simple building blocks. A number is at the bottom line
since this is the only thing a computer can understand.
A
program is defined to be “an ordered set of instructions.” Order in this
definition is a key part. Instructions run one after another, first, second,
third and so on. Instructions have a positional relationship. The whole logic
depends on this positioning. If the computer executes the fifth instructions
after the first and not the second, all our logic is gone. The processor should
ensure this ordering of instructions. A special register exists in every
processor called the program counter or the instruction pointer that ensures
this ordering. “The program counter holds the address of the next instruction
to be executed.” A number is placed in the memory cell pointed to by this
register and that number tells the processor which instruction to execute; for
example 0xEA, 255, or 152. For the processor 152 might be the add instruction.
Just this one number tells it that it has to add, where its operands are, and
where to store the result. This number is called the opcode. The
instruction pointer moves from one opcode to the next. This is how our
program executes and progresses. One instruction is picked, its operands are read
and the instruction is executed, then the next instruction is picked from the
new address in instruction pointer and so on.
Remembering 152 for the add operation or 153 for the
subtract operation is difficult. To make a simple way to remember difficult
things we associate a symbol to every number. As when we write “add” everyone
understands what we mean by it. Then we need a small program to convert this
“add” of ours to 152 for the processor. Just a simple search and replace
operation to translate all such symbols to their corresponding opcodes. We have
mapped the numeric world of the processor to our symbolic world. “Add” conveys
a meaning to us but the number 152 does not. We can say that add is closer to
the programmer’s thinking. This is the basic motive of adding more and more
translation layers up to higher level languages like C++ and Java and Visual
Basic. These symbols are called instruction mnemonics. Therefore the
mnemonic “add a to b” conveys more information to the reader. The dumb translator
that will convert these mnemonics back to the original opcodes is a key program
to be used throughout this course and is called the assembler.
1.3. INSTRUCTION GROUPS
Usual opcodes in every processor exist for moving data,
arithmetic and logical manipulations etc. However their mnemonics vary
depending on the will of the manufacturer. Some manufacturers name the
mnemonics for data movement instructions as “move,” some call it “load” and
“store” and still other names are present. But the basic set of instructions is
similar in every processor. A grouping of these instructions makes learning a
new processor quick and easy. Just the group an instruction belongs tells a lot
about the instruction.
Data Movement Instructions
These instructions are used to move data from one place to
another. These places can be registers, memory, or even inside peripheral
devices. Some examples are:
mov ax, bx
lad 1234
Arithmetic and Logic Instructions
Arithmetic instructions like addition, subtraction,
multiplication, division and Logical instructions like logical and, logical or,
logical xor, or complement are part of this group. Some examples are:
and ax, 1234
add bx,0534
add bx,[1200]
The bracketed form is a complex variation meaning to add
the data placed at address 1200. Addressing data in memory is a detailed topic
and is discussed in the next chapter.
Program Control Instructions
The instruction pointer points to the next instruction and
instructions run one after the other with the help of this register. We can say
that the instructions are tied with one another. In some situations we don’t
want to follow this implied path and want to order the processor to break its
flow if some condition becomes true instead of the spatially placed next
instruction. In certain other cases we want the processor to first execute a
separate block of code and then come back to resume processing where it left.
These are instructions that control the program execution
and flow by playing with the instruction pointer and altering its normal
behavior to point to the next instruction. Some examples are:
cmp ax, 0
jne 1234
We are changing the program flow to the instruction at
1234 address if the condition that we checked becomes true.
Special Instructions
Another group called special instructions works like the
special service commandos. They allow changing specific processor behaviors and
are used to play with it. They are used rarely but are certainly used in any
meaningful program. Some examples are:
cli sti
Where cli clears the interrupt flag and sti sets it.
Without delving deep into it, consider that the cli instruction instructs the
processor to close its ears from the outside world and never listen to what is
happening outside, possibly to do some very important task at hand, while sti
restores normal behavior. Since these instructions change the processor
behavior they are placed in the special instructions group.
1.4. INTEL IAPX88 ARCHITECTURE
Now we select a specific architecture to discuss these
abstract ideas in concrete form. We will be using IBM PC based on Intel
architecture because of its wide availability, because of free assemblers and
debuggers available for it, and because of its wide use in a variety of
domains. However the concepts discussed will be applicable on any other
architecture as well; just the mnemonics of the particular language will be
different.
Technically iAPX88 stands for “Intel Advanced Processor
Extensions 88.” It was a very successful processor also called 8088 and was
used in the very first IBM PC machines. Our discussion will revolve around 8088
in the first half of the course while in the second half we will use iAPX386
which is very advanced and powerful processor. 8088 is a 16bit processor with
its accumulator and all registers of 16 bits. 386 on the other hand, is a 32bit
processor. However it is downward compatible with iAPX88 meaning that all code
written for 8088 is valid on the 386. The architecture of a processor means the
organization and functionalities of the registers it contains and the
instructions that are valid on the processor. We will discuss the register
architecture of 8088 in detail below while its instructions are discussed in
the rest of the book at appropriate places.
1.5. HISTORY
Intel did release some 4bit processors in the beginning
but the first meaningful processor was 8080, an 8bit processor. The processor
became
popular
due to its simplistic design and versatile architecture. Based on the
experience gained from 8080, an advanced version was released as 8085. The
processor became widely popular in the engineering community again due to its
simple and logical nature.
Intel
introduced the first 16bit processor named 8088 at a time when the concept of
personal computer was evolving. With a maximum memory of 64K on the 8085, the
8088 allowed a whole mega byte. IBM embedded this processor in their personal
computer. The first machines ran at 4.43 MHz; a blazing speed at that time.
This was the right thing at the right moment. No one expected this to become
the biggest success of computing history. IBM PC XT became so popular and
successful due to its open architecture and easily available information.
The success was unexpected for the developers themselves.
As when Intel introduced the processor it contained a timer tick count which
was valid for five years only. They never anticipated the architecture to stay
around for more than five years but the history took a turn and the
architecture is there at every desk even after 25 years and the tick is to be
specially handled every now and then.
1.6. REGISTER ARCHITECTURE
The
iAPX88 architecture consists of 14 registers.
General Registers (AX, BX, CX, and DX)
The registers AX, BX, CX, and DX behave as general purpose
registers in Intel architecture and do some specific functions in addition to
it. X in their names stand for extended meaning 16bit registers. For example AX
means we are referring to the extended 16bit “A” register. Its upper and lower
byte are separately accessible as AH (A high byte) and AL (A low byte). All
general purpose registers can be accessed as one 16bit register or as two 8bit
registers. The two registers AH and AL are part of the big whole AX. Any change
in AH or AL is reflected in AX as well. AX is a composite or extended register
formed by gluing together the two parts AH and AL.
The A of AX stands for Accumulator. Even though all
general purpose registers can act as accumulator in most instructions there are
some specific variations which can only work on AX which is why it is named the
accumulator. The B of BX stands for Base because of its role in memory
addressing as discussed in the next chapter. The C of CX stands for Counter as there
are certain instructions that work with an automatic count in the CX register.
The D of DX stands for Destination as it acts as the destination in I/O
operations. The A, B, C, and D are in letter sequence as well as depict some
special functionality of the register.
SI and DI stand for source index and destination index
respectively. These are the index registers of the Intel architecture which
hold address of data and used in memory access. Being an open and flexible
architecture, Intel allows many mathematical and logical operations on these
registers as well like the general registers. The source and destination are
named because of their implied functionality as the source or the destination
in a special class of instructions called the string instructions. However
their use is not at all restricted to string instructions. SI and DI are 16bit
and cannot be used as 8bit register pairs like AX, BX, CX, and DX.
Instruction Pointer (IP)
This is the special register containing the address of the
next instruction to be executed. No mathematics or memory access can be done
through this register. It is out of our direct control and is automatically
used. Playing with it is dangerous and needs special care. Program control
instructions change the IP register.
Stack Pointer (SP)
It is a memory pointer and is used indirectly by a set of
instructions. This register will be explored in the discussion of the system
stack.
Base Pointer (BP)
It is also a memory pointer containing the address in a
special area of memory called the stack and will be explored alongside SP in
the discussion of the stack.
Flags Register
The flags register as previously discussed is not
meaningful as a unit rather it is bit wise significant and accordingly each bit
is named separately. The bits not named are unused. The Intel FLAGS register
has its bits organized as follows:
The
individual flags are explained in the following table.
Segment Registers (CS, DS, SS, and ES)
The code segment register, data segment register, stack
segment register, and the extra segment register are special registers related
to the Intel segmented memory model and will be discussed later.
1.7. OUR FIRST PROGRAM
The first program that we will write will only add three
numbers. This very simple program will clarify most of the basic concepts of
assembly language. We will start with writing our algorithm in English and then
moving on to convert it into assembly language.
English Language Version
“Program is an ordered set of instructions for the
processor.” Our first program will be instructions manipulating AX and BX in
plain English.
move 5 to ax
move 10 to bx add bx to ax move 15 to bx add bx to ax
Even in this simple reflection of thoughts in English,
there are some key things to observe. One is the concept of destination as
every instruction has a “to destination” part and there is a source before it
as well. For example the second line has a constant 10 as its source and the
register BX as its destination. The key point in giving the first program in
English is to convey that the concepts of assembly language are simple but
fine. Try to understand them considering that all above is everyday English
that you know very well and every concept will eventually be applicable to
assembly language.
Assembly Language Version
Intel could have made their assembly language exactly
identical to our program in plain English but they have abbreviated a lot of
symbols to avoid unnecessarily lengthy program when the meaning could be
conveyed with less effort. For example Intel has named their move instruction
“mov” instead of “move.” Similarly the Intel order of placing source and
destination is opposite to what we have used in our English program, just a
change of interpretation. So the Intel way of writing things is:
operation
destination, source operation destination operation source
operation
The later three variations are for instructions that have
one or both of their operands implied or they work on a single or no operand.
An implied operand means that it is always in a particular register say the
accumulator, and it need not be mentioned in the instruction. Now we attempt to
write our program in actual assembly language of the iapx88.
Assembler, Linker, and Debugger
We need an assembler to assemble this program and convert
this into executable binary code. The assembler that we will use during this
course is “Netwide Assembler” or NASM. It is a free and open source assembler.
And the tool that will be most used will be the debugger. We will use a free
debugger called “A fullscreen debugger” or AFD. These are the whole set of
To assemble we will give the following command to the
processor assuming that our input file is named EX01.ASM.
nasm ex01.asm –o ex01.com –l ex01.lst
This will produce two files EX01.COM that is our
executable file and EX01.LST that is a special listing file that we will
explore now. The listing file produced for our example above is shown below
with comments removed for neatness.
The
first column in the above listing is offset of the listed instruction in the
output file. Next column is the opcode into which our instruction was
translated. In this case this opcode is B8. Whenever we move a constant into AX
register the opcode B8 will be used. After it 0500 is appended which is the
immediate operand to this instruction. An immediate operand is an operand which
is placed directly inside the instruction. Now as the AX register is a word
sized register, and one hexadecimal digit takes 4 bits so 4 hexadecimal digits
make one word or two bytes. Which of the two bytes should be placed first in
the instruction, the least significant or the most significant? Similarly for
32bit numbers either the order can be most significant, less significant,
lesser significant, and least significant called the big-endian order used by
Motorola and some other companies or it can be least significant, more
significant, more significant, and most significant called the little -endian
order and is used by Intel. The big-endian have the argument that it is more
natural to read and comprehend while the little-endian have the argument that
this scheme places the less significant value at a lesser address and more
significant value at a higher address.
Because of this the constant 5 in our instruction was
converted into 0500 with the least significant byte of 05 first and the most
significant byte of 00 afterwards. When read as a word it is 0005 but when
written in memory it will become 0500. As the first instruction is three bytes
long, the listing file shows that the offset of the next instruction in the
file is 3. The opcode BB is for moving a constant into the BX register, and the
operand 0A00 is the number 10 in little-endian byte order. Similarly the
offsets and opcodes of the remaining instructions are shown in order. The last
instruction is placed at offset 0x10 or 16 in decimal. The size of the last
instruction is two bytes, so the size of the complete COM file becomes 18
bytes. This can be verified from the directory listing, using the DIR command,
that the COM file produced is exactly 18 bytes long.
Now
the program is ready to be run inside the debugger. The debugger shows the
values of registers, flags, stack, our code, and one or two areas of the system
memory as data. Debugger allows us to step our program one instruction at a
time and observe its effect on the registers and program data. The details of
using the AFD debugger can be seen from the AFD manual.
After loading the program in the debugger observe that the
first instruction is now at 0100 instead of absolute zero. This is the effect
of the org directive at the start of our program. The first instruction of a
COM file must be at
As a result of program execution either registers or
memory will change. Since our program yet doesn’t touch memory the only changes
will be in the registers. Keenly observe the registers AX, BX, and IP change
after every instruction. IP will change after every instruction to point to the
next instruction while AX will accumulate the result of our addition.
1.8. SEGMENTED MEMORY MODEL
Rationale
In earlier processors like 8080 and 8085 the linear memory
model was used to access memory. In linear memory model the whole memory
appears like a single array of data. 8080 and 8085 could access a total memory of
64K using the 16 lines of their address bus. When designing iAPX88 the Intel
designers wanted to remain compatible with 8080 and 8085 however 64K was too
small to continue with, for their new processor. To get the best of both worlds
they introduced the segmented memory model in 8088.
There is
also a logical argument in favor of a segmented memory model in addition to the
issue of compatibility discussed above. We have two logical parts of our
program, the code and the data, and actually there is a third part called the
program stack as well, but higher level languages make this invisible to us.
These three logical parts of a program should appear as three distinct units in
memory, but making this division is not possible in the linear memory model. The
segmented memory model does allow this distinction.
Mechanism
The segmented memory model allows multiple functional
windows into the main memory, a code window, a data window etc. The processor
sees code from the code window and data from the data window. The size of one
window is restricted to 64K. 8085 software fits in just one such window. It
sees code, data, and stack from this one window, so downward compatibility is
attained.
However the maximum memory iAPX88 can access is 1MB which
can be accessed with 20 bits. Compare this with the 64K of 8085 that were accessed
using 16 bits. The idea is that the 64K window just discussed can be moved
anywhere in the whole 1MB. The four segment registers discussed in the Intel
register architecture are used for this purpose. Therefore four windows can
exist at one time. For example one window that is pointed to by the CS register
contains the currently executing code.
To understand the concept, consider the windows of a
building. We say that a particular window is 3 feet above the floor and another
one is 20 feet above the floor. The reference point, the floor is the base of
the segment called the datum point in a graph and all measurement is done from
that datum point considering it to be zero. So CS holds the zero or the base of
code. DS holds the zero of data. Or we can say CS tells how high code from the
floor is, and DS tells how high data from the floor is, while SS tells how high
the stack is. One extra segment ES can be used if we need to access two distant
areas of memory at the same time that both cannot be seen through the same
window. ES also has special role in string instructions. ES is used as an extra
data segment and cannot be used as an extra code or stack segment.















To highlight the important thing in the
algorithm we revise it on two 4bit binary numbers. The numbers are 1101 i.e. 13
and 0101 i.e. 5. The answer should be 65 or in binary 01000001. Observe that
the answer is twice as long as the multiplier and the multiplicand. The
multiplication is shown in the following figure.
We take the first digit of the multiplier and multiply it with the multiplicand. As the digit is one the answer is the multiplicand itself. So we place the multiplicand below the bar. Before multiplying with the next digit a cross is placed at the right most place on the next line and the result is placed shifted one digit left. However since the digit is zero, the result is zero. Next digit is one, multiplying with which, the answer is 1101. We put two crosses on the next line at the right most positions and place the result there shifted two places to the left. The fourth digit is zero, so the answer 0000 is placed with three crosses to its right.


Revisiting the concept again, like the datum point of a
graph, the segment registers tell the start of our window which can be opened
anywhere in the megabyte of memory available. The window is of a fixed size of
64KB. Base and offset are the two key variables in a segmented address. Segment
tells the base while offset is added into it. The registers IP, SP, BP, SI, DI,
and BX all can contain a 16bit offset in them and access memory relative to a
segment base.
The IP register cannot work alone. It needs the CS
register to open a 64K window in the 1MB memory and then IP works to select
code from this window as offsets. IP works only inside this window and cannot
go outside of this 64K in any case. If the window is moved i.e. the CS register
is changed, IP will change its behavior accordingly and start selecting from
the new window. The IP register always works relatively, relative to the
segment base stored in the CS register. IP is a 16bit register capable of accessing
only 64K memory so how the whole megabyte can contain code anywhere. Again the
same concept is there, it can access 64K at one instance of time. As the base
is changed using the CS register, IP can be made to point anywhere in the whole
megabyte. The process is illustrated with the following diagram.
Physical Address Calculation
Now for the whole megabyte we need 20 bits while CS and IP
are both 16bit registers. We need a mechanism to make a 20bit number out of the
two 16bit numbers. Consider that the segment value is stored as a 20 bit number
with the lower four bits zero and the offset value is stored as another 20 bit
number with the upper four bits zeroed. The two are added to produce a 20bit
absolute address. A carry if generated is dropped without being stored anywhere
and the phenomenon is called address wraparound. The process is explained with
the help of the following diagram.
Therefore memory is determined by a segment-offset pair
and not alone by any one register which will be an ambiguous reference. Every
offset register is assigned a default segment register to resolve such
ambiguity. For example the program we wrote when loaded into memory had a value
of 0100 in IP register and some value say 1DDD in the CS register. Making both
20 bit numbers, the segment base is 1DDD0 and the offset is 00100 and adding
them we get the physical memory address of 1DED0 where the opcode B80500 is
placed.
Paragraph Boundaries
As the segment value is a 16bit number and four zero bits
are appended to the right to make it a 20bit number, segments can only be
defined a 16byte boundaries called paragraph boundaries. The first possible
segment value is 0000 meaning a physical base of 00000 and the next possible
value of 0001 means a segment base of 00010 or 16 in decimal. Therefore
segments can only be defined at 16 byte boundaries.
Overlapping Segments
We can also observe that in the case of our program CS,
DS, SS, and ES all had the same value in them. This is called overlapping
segments so that we can see the same memory from any window. This is the
structure of a COM file.
Using
partially overlapping segments we can produce a number of segment, offset pairs
that all access the same memory. For example 1DDD:0100 and IDED:0000 both point
to the same physical memory. To test this we can open a data window at
1DED:0000 in the debugger and change the first three bytes to “90” which is the
opcode for NOP (no operation). The change is immediately visible in the code
window which is pointed to by CS containing 1DDD. Similarly IDCD:0200 also
points to the same memory location. Consider this like a portion of wall that
three different people on three different floors are seeing through their own
windows. One of them painted the wall red; it will be changed for all of them
though their perspective is different. It is the same phenomenon occurring
here.
The segment, offset pair is called a logical address,
while the 20bit address is a physical address which is the real thing. Logical
addressing is a mechanism to access the physical memory. As we have seen three
different logical addresses accessed the same physical address.
Addressing Modes
2.1. DATA DECLARATION
The first instruction of our first assembly language
program was “mov ax, 5.” Here MOV was the opcode; AX was the destination
operand, while 5 was the source operand. The value of 5 in this case was stored
as part of the instruction encoding. In the opcode B80500, B8 was the opcode
and 0500 was the operand stored immediately afterwards. Such an operand is
called an immediate operand. It is one of the many types of operands available.
Writing
programs using just the immediate operand type is difficult. Every reasonable
program needs some data in memory apart from constants. Constants cannot be
changed, i.e. they cannot appear as the destination operand. In fact placing
them as destination is meaningless and illegal according to assembly language
syntax. Only registers or data placed in memory can be changed. So real data is
the one stored in memory, with a very few constants. So there must be a
mechanism in assembly language to store and retrieve data from memory.
To declare a part of our program as holding data instead
of instructions we need a couple of very basic but special assembler
directives. The first directive is “define byte” written as “db.”
db somevalue
As
a result a cell in memory will be reserved containing the desired value in it
and it can be used in a variety of ways. Now we can add variables instead of
constants. The other directive is “define word” or “dw” with the same syntax as
“db” but reserving a whole word of 16 bits instead of a byte. There are
directives to declare a double or a quad word as well but we will restrict
ourselves to byte and word declarations for now. For single byte we use db and
for two bytes we use dw.
To refer to this variable later in the program, we need
the address occupied by this variable. The assembler is there to help us. We
can associate a symbol with any address that we want to remember and use that
symbol in the rest of the code. The symbol is there for our own comprehension
of code. The assembler will calculate the address of that symbol using our
origin directive and calculating the instruction lengths or data declarations
in-between and replace all references to the symbol with the corresponding
address. This is just like variables in a higher level language, where the
compiler translates them into addresses; just the process is hidden from the
programmer one level further. Such a symbol associated to a point in the
program is called a label and is written as the label name followed by a colon.
2.2. DIRECT ADDRESSING
Now we will rewrite our first program such that
the numbers 5, 10, and 15 are stored as memory variables instead of constants
and we access them from there.
Using the same process to assemble as discussed before we
examine the listing file generated as a result with comments removed.
The first instruction of our program has changed from
B80500 to A11700. The opcode B8 is used to move constants into AX, while the
opcode A1 is used when moving data into AX from memory. The immediate operand
to our new instruction is 1700 or as a word 0017 (23 decimal) and from the
bottom of the listing file we can observe that this is the offset of num1. The
assembler has calculated the offset of num1 and used it to replace references
to num1 in the whole program. Also the value 0500 can be seen at offset 0017 in
the file. We can say contents of memory location 0017 are 0005 as a word.
Similarly num2, num3, and num4 are placed at 0019, 001B, and 001D addresses.
When the program is loaded in the debugger, it is loaded
at offset 0100, which displaces all memory accesses in our program. The
instruction A11700 is changed to A11701 meaning that our variable is now placed
at 0117 offset. The instruction is shown as mov ax, [0117]. Also the data
window can be used to verify that offset 0117 contains the number 0005.
Execute
the program step by step and examine how the memory is read and the registers
are updated, how the instruction pointer moves forward, and how the result is
saved back in memory. Also observe inside the debugger code window below the
code for termination, that the debugger is interpreting our data as code and
showing it as some meaningless instructions. This is because the debugger sees
everything as code in the code window and cannot differentiate our declared
data from opcodes. It is our responsibility that we terminate execution before
our data is executed as code.
Also
observe that our naming of num1, num2, num3, and num4 is no longer there inside
the debugger. The debugger is only showing the numbers 0117, 0119, 011B, and
011D. Our numerical machine can only work with numbers. We used symbols for our
ease to label or tag certain positions in our program. The assembler converts
these symbols into the appropriate numbers automatically. Also observe that the
effect of “dw” is to place 5 in two bytes as 0005. Had we used “db” this would
have been stored as 05 in one byte.
Given the fact that the assembler knows only numbers we
can write the same program using a single label. As we know that num2 is two
ahead of num1, we can use num1+2 instead of num2 and let the assembler
calculate the sum during assembly process.
Every location is accessed with reference to num1 in this
example. The expression “num1+2” comprises of constants only and can be
evaluated at the time of assembly. There are no variables involved in this
expression. As we open the program inside the debugger we see a verbatim copy
of the previous program. There is no difference at all since the assembler
catered for the differences during assembly. It calculated 0117+2=0119 while in
the previous it directly knew from the value of num2 that it has to write 0119,
but the end result is a ditto copy of the previous execution.
Another way to declare the above data and produce exactly
same results is shown in the following example.
The method used to access memory in the above examples is
called direct addressing. In direct addressing the memory address is fixed and
is given in the instruction. The actual data used is placed in memory and now
that data can be used as the destination operand as well. Also the source and
destination operands must have the same size. For example a word defined memory
is read in a word sized register. A last observation is that the data 0500 in
memory was corrected to 0005 when read in a register. So registers contain data
in proper order as a word.
A last variation using direct addressing shows that we can
directly add a memory variable and a register instead of adding a register into
another that we were doing till now.
The
opcode of add is changed because the destination is now a memory location
instead of a register. No other significant change is seen in the listing file. Inside the debugger we observe that few
opcodes are longer now and the location num1 is now translating to 0119 instead
of 0117. This is done automatically by the assembler as a result of using
labels instead of
hard
coding addresses. During execution we observe that the word data as it is read
into a register is read in correct order. The significant change in this
example is that the destination of addition is memory. Method to access memory
is direct addressing, whether it is the MOV instruction or the ADD instruction.
The first two instructions of the last program read a
number into AX and placed it at another memory location. A quick thought
reveals that the following might be a possible single instruction to replace
the couple.
mov [num1+6], [num1]
; ILLEGAL
However this form is illegal and not allowed on the Intel
architecture. None of the general operations of mov add, sub etc. allow moving
data from memory to memory. Only register to register, register to memory,
memory to register, constant to memory, and constant to register operations are
allowed. The other register to constant, memory to constant, and memory to
memory are all disallowed. Only string instructions allow moving data from
memory to memory and will be discussed in detail later. As a rule one
instruction can have at most one operand in brackets, otherwise assembler will
give an error.
2.3. SIZE MISMATCH ERRORS
If
we change the directive in the last example from DW to DB, the program will
still assemble and debug without errors, however the results will not be the
same as expected. When the first operand is read 0A05 will be read in the
register which was actually two operands place in consecutive byte memory locations.
The second number will be read as 000F which is the zero byte of num4 appended
to the 15 of num3. The third number will be junk depending on the current state
of the machine. According to our data declaration the third number should be at
0114 but it is accessed at 011D calculated with word offsets. This is a logical
error of the program. To keep the declarations and their access synchronized is
the responsibility of the programmer and not the assembler. The assembler
allows the programmer to do everything he wants to do, and that can possibly
run on the processor. The assembler only keeps us from writing illegal
instructions which the processor cannot execute. This is the difference between
a syntax error and a logic error. So the assembler and debugger have both done
what we asked them to do but the programmer asked them to do the wrong chore.
The programmer is responsible for accessing the data as
word if it was declared as a word and accessing it as a byte if it was declared
as a byte. The word case is shown in lot of previous examples. If however the
intent is to treat it as a byte the following code shows the appropriate way.
Inside the debugger we observe that the AL register takes
appropriate values and the sum is calculated and stored in num1+3. This time
there is no alignment or synchronization error. The key thing to understand
here is that the processor does not match defines to accesses. It is the
programmer’s responsibility. In general assembly language gives a lot of power
to the programmer but power comes with responsibility. Assembly language
programming is not a difficult task but a responsible one.
In
the above examples, the processor knew the size of the data movement operation
from the size of the register involved, for example in “mov ax, [num1]” memory
can be accessed as byte or as word, it has no hard and fast size, but the AX
register tells that this operation has to be a word operation. Similarly in
“mov al, [num1]” the AL register tells that this operation has to be a byte
operation. However in “mov ax, bl” the AX register tells that the operation has
to be a word operation while BL tells that this has to be a byte operation. The
assembler will declare that this is an illegal instruction. A 5Kg bag cannot
fit inside a 1Kg bag and according to Intel a 1Kg cannot also fit in a 5Kg bag.
They must match in size. The instruction “mov [num1], [num2]” is illegal as
previously discussed not because of data movement size but because memory to
memory moves are not allowed at all.
The instruction “mov [num1], 5” is legal but there is no
way for the processor to know the data movement size in this operation. The
variable num1 can be treated as a byte or as a word and similarly 5 can be
treated as a byte or as a word. Such instructions are declared ambiguous by the
assembler. The assembler has no way to guess the intent of the programmer as it
previously did using the size of the register involved but there is no register
involved this time. And memory is a linear array and label is an address in it.
There is no size associated with a label. Therefore to resolve its ambiguity we
clearly tell our intent to the assembler in one of the following ways.
mov byte
[num1], 5 mov word [num1], 5
2.4. REGISTER INDIRECT ADDRESSING
We have done very elementary data access till
now. Assume that the numbers we had were 100 and not just three. This way of
adding them will cost us 200 instructions. There must be some method to do a
task repeatedly on data placed in consecutive memory cells. The key to this is
the need for some register that can hold the address of data. So that we can
change the address to access some other cell of memory using the same
instruction. In direct addressing mode the memory cell accessed was fixed
inside the instruction. There is another method in which the address can be
placed in a register so that it can be changed. For the following example we
will take 10 instead of 100 numbers but the algorithm is extensible to
any size.
There are four registers in iAPX88 architecture that can
hold address of data and they are BX, BP, SI, and DI. There are minute
differences in their working which will be discussed later. For the current
example, we will use the BX register and we will take just three numbers and
extend the concept with more numbers in later examples.
Inside
the debugger we observe that the first instruction is “mov bx, 011C.” A
constant is moved into BX. This is because we did not use the square brackets
around “num1.” The address of “num1” has moved to 011C because the code size
has changed due to changed instructions. In the second instruction BX points to
011C and the value read in AX is 0005 which can be verified from the data
window. After the addition BX points to 011E containing 000A, our next word,
and so on. This way the BX register points to our words one after another and
we can add them using the same instruction “mov ax, [bx]” without fixing the
address of our data in the instructions. We can also subtract from BX to point
to previous cells. The address to be accessed is now in total program control.
One thing that we needed in our problem to add hundred
numbers was the capability to change address. The second thing we need is a way
to repeat the same instruction and a way to know that the repetition is done a
100 times, a terminal condition for the repetition. For the task we are
introducing two new instructions that you should read and understand as simple
English language concepts. For simplicity only 10 numbers are added in this
example. The algorithm is extensible to any size.
The CX register is used as a counter in this example, BX
contains the changing address, while AX accumulates the result. We have formed
a loop in assembly language that executes until its condition remains true.
Inside the debugger we can observe that the subtract instruction clears the
zero flag the first nine times and sets it on the tenth time. While the jump
instruction moves execution to address l1 the first nine times and to the
following line the tenth time. The jump instruction breaks program flow.
The JNZ instruction is from the program control
group and is a conditional jump, meaning that if the condition NZ is true
(ZF=0) it will jump to the address mentioned and otherwise it will progress to
the next instruction. It is a selection between two paths. If the condition is
true go right and otherwise go left. Or we can say if the weather is hot, go
this way, and if it is cold, go this way. Conditional jump is the most
important instruction, as it gives the processor decision making capability, so
it must be given a careful thought. Some processors call it branch, probably a
more logical name for it, however the
functionality is same. Intel chose to name it “jump.”
An important thing in the above example is that a register
is used to reference memory so this form of access is called register indirect
memory access. We used the BX register for it and the B in BX and BP stands for
base therefore we call register indirect memory access using BX or BP, “based
addressing.” Similarly when SI or DI is used we name the method “indexed
addressing.” They have the same functionality, with minor differences because
of which the two are called base and index. The differences will be explained
later, however for the above example SI or DI could be used as well, but we
would name it indexed addressing instead of based addressing.
2.5. REGISTER + OFFSET ADDRESSING
Direct addressing and indirect addressing using a single
register are two basic forms of memory access. Another possibility is to use
different combinations of direct and indirect references. In the above example
we used BX to access different array elements which were placed consecutively
in memory like an array. We can also place in BX only the array index and not
the exact address and form the exact address when we are going to access the
actual memory. This way the same register can be used for accessing different
arrays and also the register can be used for index comparison like the
following example does.
Inside the debugger we observe that the memory access
instruction is shown as “mov ax, [011F+bx]” and the actual memory accessed is
the one whose address is the sum of 011F and the value contained in the BX
register. This form of access is of the register indirect family and is called
base + offset or index + offset depending on whether BX or BP is used or SI or
DI is used.
All the addressing mechanisms in iAPX88 return a number
called effective address. For example in base + offset
addressing, neither the base nor the offset alone tells the desired cell
in memory to be accessed. It is only after the addition is done that the
processor knows which cell to be accessed. This number which came as the result
of addition is called the effective address. But the effective address is just
an offset and is meaningless without a segment. Only after the segment is
known, we can form the physical address that is needed to access a memory cell.
We discussed the segmented memory model of iAPX88 in
reasonable detail at the end of previous chapter. However during the discussion
of addressing modes we have not seen the effect of segments. Segmentation is
there and it’s all happening relative to a segment base. We saw DS, CS, SS, and
ES
In
case of data, there is a bit relaxation and nothing is tied. Rather there is a
default association which can be overridden. In the case of register indirect
memory access, if the register used is one of SI, DI, or BX the default segment
is DS. If however the register used is BP the default segment used is SS. The
stack segment has a very critical and fine use and there is a reason why BP is
attached to SS by default. However these will be discussed in detail in the
chapter on stack. IP is tied to CS while SP is tied to SS. The association of
these registers cannot be changed; they are locked with no option. Others are
not locked and can be changed.
To
override the association for one instruction of one of the registers BX, BP, SI
or DI, we use the segment override prefix. For example “mov ax, [cs:bx]”
associates BX with CS for this one instruction. For the next instruction the
default association will come back to act. The processor places a special byte
before the instruction called a prefix, just like prefixes and suffixes in
English language. No prefix is needed or placed for default association. For
example for CS the byte 2E is placed and for ES the byte 26 is placed. Opcode
has not changed, but the prefix byte has modified the default association to
association with the desired segment register for this one instruction.
In
all our examples, we never declared a segment or used it explicitly, but everything
seemed to work fine. The important thing to note is that CS, DS, SS, and ES all
had the same value. The value itself is not important but the fact that all had
the same value is important. All four segment windows exactly overlap. Whatever
segment register we use the same physical memory will be accessed. That is why
everything was working without the mention of a single segment register. This
is the formation of COM files in IBM PC. A single segment contains code, data,
and the stack. This format is operating system dependant, in our case defined
by DOS. And our operating system defines the format of COM files such that all
segments have the same value. Thus the only meaningful thing that remains is
the offset.
For example if BX=0100, SI=0200, and CS=1000 and the
memory access under consideration is [cs:bx+si+0x0700], the effective address
formed is bx+si+0700 = 0100 + 0200 + 0700 = 0A00. Now multiplying the segment
value by 16 makes it 10000 and adding the effective address 00A00 forms the
physical address 10A00.
2.7. ADDRESS WRAPAROUND
There
are two types of wraparounds. One is within a single segment and the other is
inside the whole physical memory. Segment wraparound occurs when during the
effective address calculation a carry is generated. This carry is dropped
giving the effect that when we try to access beyond the segment limit, we are
actually wrapped around to the first cell in the segment. For example if
BX=9100, DS=1500 and the access is [bx+0x7000] we form the effective address
9100 + 7000 = 10100. The carry generated is dropped forming the actual
effective address of 0100. Just like a circle when we reached the end we
started again from the beginning. An arc at 370 degrees is the same as an arc
at 10 degrees. We tried to cross the segment boundary and it pushed us back to
the start. This is called segment wraparound. The physical address in the above
example will be 15100.
The same can also happen at the time of physical address
calculation. For example BX=0100, DS=FFF0 and the access under consideration is
[bx+0x0100]. The effective address will be 0200 and the physical address will
2.8. ADDRESSING MODES SUMMARY
The iAPX88 processor supports seven modes of memory
access. Remember that immediate is not an addressing mode but an operand type.
Operands can be immediate, register, or memory. If the operand is memory one of
the seven addressing modes will be used to access it. The memory access
mechanisms can also be written in the general form “base + index + offset” and
we can define the possible addressing modes by saying that any one, two, or
none can be skipped from the general form to form a legal memory access.
There are a few common mistakes done in forming a valid
memory access. Part of a register cannot be used to access memory. Like BX is
allowed to hold an address but BL or BH are not. Address is 16bit and must be
contained in a 16bit register. BX-SI is not possible. The only thing that we
can do is addition of a base register with an index register. Any other
operation is disallowed. BS+BP and SI+DI are both disallowed as we cannot have
two base or two index registers in one memory access. One has to be a base register
and the other has to be an index register and that is the reason of naming them
differently.
Direct
A fixed offset is given in brackets and the memory at that
offset is accessed. For example “mov [1234], ax” stores the contents of the AX
registers in two bytes starting at address 1234 in the current data segment.
The instruction “mov [1234], al” stores the contents of the AL register in the
byte at offset 1234.
Based Register Indirect
A base register is used in brackets and the actual address
accessed depends on the value contained in that register. For example “mov
[bx], ax” moves the two byte contents of the AX register to the address
contained in the BX register in the current data segment. The instruction “mov
[bp], al” moves the one byte content of the AL register to the address
contained in the BP register in the current stack segment.
Indexed Register Indirect
An index register is used in brackets and the actual
address accessed depends on the value contained in that register. For example
“mov [si], ax” moves the contents of the AX register to the word starting at
address contained in SI in the current data segment. The instruction “mov [di],
ax” moves the word contained in AX to the offset stored in DI in the current
data segment.
Based Register Indirect + Offset
A base register is used with a constant offset in this
addressing mode. The value contained in the base register is added with the
constant offset to get the effective address. For example “mov [bx+300], ax”
stores the word contained in AX at the offset attained by adding 300 to BX in
the current data segment. The instruction “mov [bp+300], ax” stores the word in
AX to the offset attained by adding 300 to BP in the current stack segment.
An index register is used with a constant offset in this addressing
mode. The value contained in the index register is added with the constant
offset to get the effective address. For example “mov [si+300], ax” moves the
word contained in AX to the offset attained by adding 300 to SI in the current
data segment and the instruction “mov [di+300], al” moves the byte contained in
AL to the offset attained by adding 300 to DI in the current data segment.
Base + Index
One base and one index register is used in this addressing
mode. The value of the base register and the index register are added together
to get the effective address. For example “mov [bx+si], ax” moves the word
contained in the AX register to offset attained by adding BX and SI in the
current data segment. The instruction “mov [bp+di], al” moves the byte
contained in AL to the offset attained by adding BP and DI in the current stack
segment. Observe that the default segment is based on the base register and not
on the index register. This is why base registers and index registers are named
separately. Other examples are “mov [bx+di], ax” and “mov [bp+si], ax.” This
method can be used to access a two dimensional array such that one dimension is
in a base register and the other is in an index register.
Base + Index + Offset
This is the most complex addressing method and is
relatively infrequently used. A base register, an index register, and a
constant offset are all used in this addressing mode. The values of the base
register, the index register, and the constant offset are all added together to
get the effective address. For example “mov [bx+si+300], ax” moves the word
contents of the AX register to the word in memory starting at offset attained
by adding BX, SI, and 300 in the current data segment. Default segment
association is again based on the base register. It might be used with the
array base of a two dimensional array as the constant offset, one dimension in
the base register and the other in the index register. This way all calculation
of location of the desired element has been delegated to the processor.
3.1. COMPARISON AND
CONDITIONS
Conditional
jump was introduced in the last chapter to loop for the addition of a fixed
number of array elements. The jump was based on the zero flag. There are many
other conditions possible in a program. For example an operand can be greater
than another operand or it can be smaller. We use comparisons and boolean
expressions extensively in higher level languages. They must be available is
some form in assembly language, otherwise they could not possibly be made
available in a higher level language. In fact they are available in a very fine
and purified form.
The
basic root instruction for all comparisons is CMP standing for compare. The
operation of CMP is to subtract the source operand from the destination
operand, updating the flags without changing either the source or the
destination. CMP is one of the key instructions as it introduces the capability
of conditional routing in the processor.
A closer thought reveals that with
subtraction we can check many different conditions. For example if a larger
number is subtracted from a smaller number then borrow is needed. The carry
flag plays the role of borrow during the subtraction operation. And in this
condition the carry flag will be set. If two equal numbers are subtracted the
answer is zero and the zero flag will be set. Every significant relation
between the destination and source is evident from the sign flag, carry flag,
zero flag, and the overflow flag. CMP is meaningless without a conditional jump
immediately following it.
Another important distinction at this
point is the difference between signed and unsigned numbers. In unsigned
numbers only the magnitude of the number is important, whereas in signed
numbers both the magnitude and the sign are important. For example -2 is
greater than -3 but 2 is smaller than 3. The sign has affected our comparisons.
Inside the computer signed numbers
are represented in two’s complement notation. In essence a number in this
representation is still a number, just that now our interpretation of this
number will be signed. Whether we use jump above and below or we use jump
greater or less will convey our intention to the processor. The jump above and
greater operations at first sight seem to be doing the same operation, and
similarly below and less operations seem to be similar. However for signed
numbers JG and JL will work properly and for unsigned JA and JB will work
properly and not the other way around.
It is important to note that at the
time of comparison, the intent of the programmer to treat the numbers as signed
or unsigned is not clear. The subtraction in CMP is a normal subtraction. It is
only after the comparison, during the conditional jump operation, that the
intent is conveyed. At that time with a specific combination of flags checked
the intent is satisfied.
For
example a number 2 is represented in a word as 0002 while the number -2 is
represented as FFFE. In a byte they would be represented as 02 and FE. Now both
have the same magnitude however the different sign has caused very different
representation in two’s complement form. Now if the intent is to use FFFE or
decimal 65534 then the same data would be placed in the word as in case of -2.
In fact if -2 and 65534 are compared the processor will set the zero flag
signaling that they are exactly equal. As regards an unsigned comparison the number
65534 is much greater than 2.
So
if a JA is taken after comparing -2 in the destination with 2 in the source the
jump will be taken. If however JG is used after the same comparison the jump
will not be taken as it will consider the sign and with the sign -2 is smaller
than 2. The key idea is that -2 and 65534 were both stored in memory in the same
form. It was the interpretation that treated it as a signed or as an unsigned
number.
The unsigned comparisons see the numbers as 0 being the
smallest and 65535 being the largest with the order that 0 < 1 < 2 … <
65535. The signed comparisons see the number -32768 which has the same memory
representation as 32768 as the smallest number and 32767 as the largest with
the order -32768 < -32767 < … < -1 < 0 < 1 < 2 < … <
32767. All the negative numbers have the same representation as an unsigned
number in the range 32768 … 65535 however the signed interpretation of the
signed comparisons makes them be treated as negative numbers smaller than zero.
All
meaningful situations both for signed and unsigned numbers that occur after a
comparison are detailed in the following table.
3.2. CONDITIONAL JUMPS
For every interesting or meaningful situation of flags, a
conditional jump is there. For example JZ and JNZ check the zero flag. If in a
comparison both operands are same, the result of subtraction will be zero and
the zero flag will be set. Thus JZ and JNZ can be used to test equality. That
is why there are renamed versions JE and JNE read as jump if equal or jump if
not equal. They seem more logical in writing but mean exactly the same thing
with the same opcode. Many jumps are renamed with two or three names for the
same jump, so that the appropriate logic can be conveyed in assembly language
programs. This renaming is done by Intel and is a standard for iAPX88. JC and
JNC test the carry flag. For example we may need to test whether there was an
overflow in the last unsigned addition or subtraction. Carry flag will also be
set if two unsigned numbers are subtracted and the first is smaller than the
second. Therefore the renamed versions JB, JNAE, and JNB, JAE are there
standing for jump if below, jump if not above or equal, jump if not below, and
jump if above or equal respectively. The operation of all jumps can be seen
from the following table.
The CMP instruction sets the flags reflecting the relation
of the destination to the source. This is important as when we say jump if
above, then what is above what. The destination is above the source or the
source is above the destination.
The JA and JB instructions are related to unsigned
numbers. That is our interpretation for the destination and source operands is
unsigned. The 16th bit holds data and not the sign. In the JL and JG
instructions standing for jump if lower and jump if greater respectively, the
interpretation is signed. The 16th bit holds the sign and not the data. The
difference between them will be made clear as an elaborate example will be
given to explain the difference.
One
jump is special that it is not dependant on any flag. It is JCXZ, jump if the
CX register is zero. This is because of the special treatment of the CX
register as a counter. This jump is regardless of the zero flag. There is no
counterpart or not form of this instruction.
The adding numbers example of the last chapter can be a
little simplified using the compare instruction on the BX register and
eliminating the need for a separate counter as below.
With conditional branching in hand, there are just a few
small things left in assembly language that fills some gaps. Now there is just
imagination and the skill to conceive programs that can make you write any
program.
3.3. UNCONDITIONAL JUMP
Till now we have been placing data at the end of code.
There is no such restriction and we can define data anywhere in the code.
Taking the previous example, if we place data at the start of code instead of
at the end and we load our program in the debugger. We can see our data placed
at the start but the debugger is intending to start execution at our data. The
COM file definition said that the first executable instruction is at offset
0100 but we have placed data there instead of code. So the debugger will try to
interpret that data as code and showed whatever it could make up out of those
opcodes.
We introduce a new instruction called JMP. It is the
unconditional jump that executes regardless of the state of all flags. So we
write an unconditional jump as the very first instruction of our program and
jump to the next instruction that follows our data declarations. This time 0100
contains a valid first instruction of our program.
3.4. RELATIVE ADDRESSING
Inside the debugger the instruction is shown as JMP 0119
and the location 0119 contains the original first instruction of the logic of
our program. This jump is unconditional, it will always be taken. Now looking
at the opcode we see F21600 where F2 is the opcode and 1600 is the operand to
it. 1600 is 0016 in proper word order. 0119 is not given as a parameter rather
0016 is given.
This is position relative addressing in contrast to
absolute addressing. It is not telling the exact address rather it is telling
how much forward or backward to go from the current position of IP in the
current code segment. So the instruction means to add 0016 to the IP register.
At the time of execution of the first instruction at 0100 IP was pointing to
the next instruction at 0103, so after adding 16 it became 0119, the desired
target location. The mechanism is important to know, however all calculations
in this mechanism are done by the assembler and by the processor. We just use a
label with the JMP instruction and are ensured that the instruction at the
target label will be the one to be executed.
3.5. TYPES OF JUMP
The three types of jump, near, short, and far, differ in
the size of instruction and the range of memory they can jump to with the
smallest short form of two bytes and a range of just 256 bytes to the far form
of five bytes and a range covering the whole memory.
Near Jump
When the relative address stored with the instruction is
in 16 bits as in the last example the jump is called a near jump. Using a near
jump we can jump anywhere within a segment. If we add a large number it will
wrap around to
the
lower part. A negative number actually is a large number and works this way
using the wraparound behavior.
Short Jump
If the offset is stored in a single byte as in 75F2 with
the opcode 75 and operand F2, the jump is called a short jump. F2 is added to
IP as a signed byte. If the byte is negative the complement is negated from IP
otherwise the byte is added. Unconditional jumps can be short, near, and far.
The far type is yet to be discussed. Conditional jumps can only be short. A
short jump can go +127 bytes ahead in code and -128 bytes backwards and no
more. This is the limitation of a byte in singed representation.
Far Jump
Far jump
is not position relative but is absolute. Both segment and offset must be given
to a far jump. The previous two jumps were used to jump within a segment.
Sometimes we may need to go from one code segment to another, and near and
short jumps cannot take us there. Far jump must be used and a two byte segment
and a two byte offset are given to it. It loads CS with the segment part and IP
with the offset part. Execution therefore resumes from that location in
physical memory. The three instructions that have a far form are JMP, CALL, and
RET, are related to program control. Far capability makes intra segment control
possible.
3.6. SORTING EXAMPLE
Moving ahead from our example of adding numbers we
progress to a program that can sort a list of numbers using the tools that we
have accumulated till now. Sorting can be ascending or descending like if the
largest number comes at the top, followed by a smaller number and so on till
the smallest number the sort will be called descending. The other order
starting with the smallest number and ending at the largest is called ascending
sort. This is a common problem and many algorithms have been developed to solve
it. One simple algorithm is the bubble sort algorithm.
In
this algorithm we compare consecutive numbers. If they are in required order
e.g. if it is a descending sort and the first is larger then the second, then
we leave them as it is and if they are not in order, we swap them. Then we do
the same process for the next two numbers and so on till the last two are
compared and possibly swapped.
A
complete iteration is called a pass over the array. We need N passes at least
in the simplest algorithm if N is the number of elements to be sorted. A finer
algorithm is to check if any swap was done in this pass and stop as soon as a
pass goes without a swap. The array is now sorted as every pair of elements is
in order.
For example if our list of numbers is 60, 55, 45, and 58
and we want to sort them in ascending order, the first comparison will be of 60
and 55 and as the order will be reversed to 55 and 60. The next comparison will
be of 60 and 45 and again the two will be swapped. The next comparison of 60
and 58 will also cause a swap. At the end of first pass the numbers will be in
order of 55, 45, 58, and 60. Observe that the largest number has bubbled down
to the bottom. Just like a bubble at bottom of water. In the next pass 55 and
45 will be swapped. 55 and 58 will not be swapped and 58 and 60 will also not
be swapped. In the next pass there will be no swap as the elements are in order
i.e. 45, 55, 58, and 60. The passes will be stopped as the last pass did not cause
any swap. The application of bubble sort on these numbers is further explained
with the following illustration.
Inside the debugger we observe that the JBE is changed to
JNA due to the same reason as discussed for JNE and JNZ. The passes change the
data in the same manner as we presented in our illustration above. If JBE in
the code is changed to JAE the sort will change from ascending to descending.
For signed numbers we can use JLE and JGE respectively for ascending and
descending sort.
To clarify the difference of signed and unsigned jumps we
change the data array in the last program to include some negative numbers as
well. When JBE will be used on this data, i.e. with unsigned interpretation of
the data and an ascending sort, the negative numbers will come at the end after
the largest positive number. However JLE will bring the negative numbers at the
very start of the list to bring them in proper ascending order according to a
signed interpretation, even though they are large in magnitude. The data used
is shown as below.
data:
|
dw 60, 55, 45, 50, -40,
-35, 25, 30, 10, 0
|
This
data includes some signed numbers as well. The JBE instruction will treat this
data as an unsigned number and will cater only for the magnitude ignoring the
sign. If the program is loaded in the debugger, the numbers will appear in
their hexadecimal equivalent. The two numbers -40 and -35 are especially
important as they are represented as FFD8 and FFDD. This data is not telling
whether it is signed or unsigned. Our interpretation will decide whether it is
a very large unsigned number or a signed number in two’s complement form.
If the sorting algorithm is applied on the above data with
JBE as the comparison instruction to sort in ascending order with unsigned
interpretation, observe the comparisons of the two numbers FFD8 and FFDD. For
example it will decide that FFDD > FFD8 since the first is larger in
magnitude. At the end of sorting FFDD will be at the end of the list being
declared the largest number and FFD8 will precede it to be the second largest.
If however the comparison instruction is changed to JLE
and sorting is done on the same data it works similarly except on the two
numbers FFDD and FFD8. This time JLE declares them to be smaller than every
other number and also declares FFDD < FFD8. At the end of sorting, FFDD is
If
the required interpretation was of signed numbers the result produced by JLE is
correct and if the required interpretation was of unsigned numbers the result
produced by JBE is correct. This is the very difference between signed and
unsigned integers in higher level languages, where the compiler takes the
responsibility of making the appropriate jump depending on the type of integer
used. But it is only at this level that we can understand the actual mechanism
going on. In assembly language, use of proper jump is the responsibility of the
programmer, to convey the intentions to use the data as signed or as unsigned.
The remaining possibilities of signed descending sort and
unsigned descending sort can be done on the same lines and are left as an
exercise. Other conditional jumps work in the same manner and can be studied
from the reference at the end. Several will be discussed in more detail when
they are used in subsequent chapters.
Bit Manipulations
4.1. MULTIPLICATION
ALGORITHM
With the
important capability of decision making in our repertoire we move on to the
discussion of an algorithm, which will help us uncover an important set of
instructions in our processor used for bit manipulations.
Multiplication is a common process
that we use, and we were trained to do in early schooling. Remember multiplying
by a digit and then putting a cross and then multiplying with the next digit
and putting two crosses and so on and summing the intermediate results in the
end. Very familiar process but we never saw the process as an algorithm, and we
need to see it as an algorithm to convey it to the processor.
We take the first digit of the multiplier and multiply it with the multiplicand. As the digit is one the answer is the multiplicand itself. So we place the multiplicand below the bar. Before multiplying with the next digit a cross is placed at the right most place on the next line and the result is placed shifted one digit left. However since the digit is zero, the result is zero. Next digit is one, multiplying with which, the answer is 1101. We put two crosses on the next line at the right most positions and place the result there shifted two places to the left. The fourth digit is zero, so the answer 0000 is placed with three crosses to its right.
Observe the
beauty of binary base, as no real multiplication is needed at the digit level.
If the digit is 0 the answer is 0 and if the digit is 1 the answer is the
multiplicand itself. Also observe that for every next digit in the multiplier
the answer is written shifted one more place to the left. No shifting for the
first digit, once for the second, twice for the third and thrice for the fourth
one. Adding all the intermediate answers the result is 01000001=65 as desired.
Crosses are treated as zero in this addition.
Before
formulating the algorithm for this problem, we need some more instructions that
can shift a number so that we use this instruction for our multiplicand
shifting and also some way to check the bits of the multiplier one by one.
4.2. SHIFTING AND
ROTATIONS
The set
of shifting and rotation instructions is one of the most useful set in any
processor’s instruction set. They simplify really complex tasks to a very
neat
and concise algorithm. The following shifting and rotation operations are
available in our processor.
Shift Logical Right (SHR)
The shift logical right operation inserts a zero from the
left and moves every bit one position to the right and copies the rightmost bit
in the carry flag. Imagine that there is a pipe filled to capacity with eight
balls. The pipe is open from both ends and there is a basket at the right end
to hold anything dropping from there. The operation of shift logical right is
to force a white ball from the left end. The operation is depicted in the
following illustration.
White balls represent zero bits while black balls
represent one bits. Sixteen bit shifting is done the same way with a pipe of
double capacity.
Shift Logical Left (SHL) / Shift Arithmetic
Left (SAL)
The shift logical left operation is the exact opposite of
shift logical right. In this operation the zero bit is inserted from the right
and every bit moves one position to its left with the most significant bit
dropping into the carry flag. Shift arithmetic left is just another name for
shift logical left. The operation is again exemplified with the following
illustration of ball and pipes.
Shift Arithmetic Right (SAR)
A signed number holds the sign in its most significant
bit. If this bit was one a logical right shifting will change the sign of this
number because of insertion of a zero from the left. The sign of a signed
number should not change because of shifting.
The operation of shift arithmetic right is therefore to
shift every bit one place to the right with a copy of the most significant bit
left at the most significant place. The bit dropped from the right is caught in
the carry basket. The sign bit is retained in this operation. The operation is
further illustrated below.
The left shifting operation is basically multiplication by
2 while the right shifting operation is division by two. However for signed
numbers division by two can be accomplished by using shift arithmetic right and
not shift logical right. The left shift operation is equivalent to
multiplication except when an important bit is dropped from the left. The
overflow flag will signal this condition if it occurs and can be checked with
JO. For division by 2 of a signed number logical right shifting will give a wrong
answer for a negative number as the zero inserted from the left will change its
sign. To retain the sign flag and still effectively divide by two the shift
arithmetic right instruction must be used on signed numbers.
Rotate Right (ROR)
In the rotate right operation every bit moves one position
to the right and the bit dropped from the right is inserted at the left. This
bit is also copied into the carry flag. The operation can be understood by
imagining that the pipe used for shifting has been molded such that both ends
coincide. Now when the first ball is forced to move forward, every ball moves
one step forward with the last ball entering the pipe from its other end
occupying the first ball’s old position. The carry basket takes a snapshot of
this ball leaving one end of the pipe and entering from the other.
Rotate Left (ROL)
In the operation of rotate left instruction, the most
significant bit is copied to the carry flag and is inserted from the right,
causing every bit to move one position to the left. It is the reverse of the
rotate right instruction. Rotation can be of eight or sixteen bits. The
following illustration will make the concept clear using the same pipe and
balls example.






















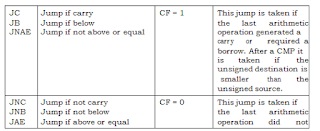













No comments:
Post a Comment